csp-j 历年真题
注意事项
2024年CSP-J组复赛
P11227 [CSP-J 2024] 扑克牌
题目描述
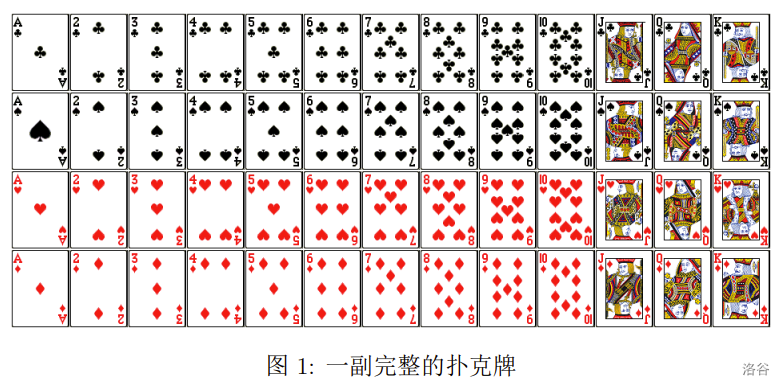
输入格式
输出格式
输入输出样例 #1
输入 #1
1
SA输出 #1
51输入输出样例 #2
输入 #2
4
DQ
H3
DQ
DT输出 #2
49说明/提示
| 测试点编号 | 特殊性质 | |
|---|---|---|
| A | ||
| ^ | ||
| ^ | B | |
| ^ | 无 |
代码
P11228 [CSP-J 2024] 地图探险
题目描述
1.
2.
输入格式
输出格式
输入输出样例 #1
输入 #1
2
1 5 4
1 1 2
....x
5 5 20
1 1 0
.....
.xxx.
.x.x.
..xx.
x....输出 #1
3
13说明/提示
1.
2.
3.
4.
5.
| 测试点编号 | 特殊性质 | |||
|---|---|---|---|---|
| 无 | ||||
| ^ | ^ | ^ | ^ | |
| ^ | ^ | |||
| ^ | ^ | ^ | ^ | |
| 地图上所有位置均为空地 | ||||
| ^ | ^ | ^ | 无 | |
| ^ | 地图上所有位置均为空地 | |||
| ^ | ^ | ^ | 无 | |
| ^ | ^ | ^ | ^ | |
| ^ | ^ | ^ | ^ |
代码
P11229 [CSP-J 2024] 小木棍
题目描�述
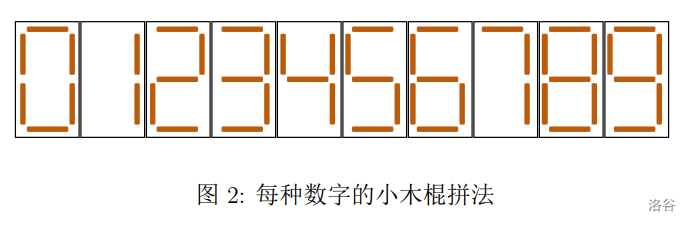
输入格式
输出格式
5
1
2
3
6
18-1
1
7
6
208说明/提示
| 测试点编号 | 特殊性质 | |
|---|---|---|
| 无 | ||
| ^ | ||
| A | ||
| ^ | ||
| B | ||
| ^ | ||
| 无 | ||
| ^ |
代码
该题为:求n根木棍组成的无前导0的所有可能的数值中的最小数值
要想使最值数值最小,首先考虑让数字位数尽量少。朴素地想,每位数字使用的木棍越多,数字位数越少。一位数字最多使用7根木棍,摆成“8”。
我们可以考虑,将n根木棍不断摆出数字“8”,看最后剩下几根木棍,再做处理。
每次摆出数字“8”用7根木棍,最后剩下的木棍数量为n%7
已知构成每种数字的木棍数,以及距离摆成8还差几根木棍(7减去数字的木棍数)
表1:根据上表可知,n根木棍可以摆出的数值最小的数字的位数为d = ⌈ n / 7 ⌉ d = \lceil n/7 \rceild=⌈n/7⌉
,n为1时无法摆成数字。
| 数字 | 木棍数 | 距离摆成8还差几根木棍 |
|---|---|---|
| 0 | 6 | 1 |
| 1 | 2 | 5 |
| 2 | 5 | 2 |
| 3 | 5 | 2 |
| 4 | 4 | 3 |
| 5 | 5 | 2 |
| 6 | 6 | 1 |
| 7 | 3 | 4 |
| 8 | 7 | 0 |
| 9 | 6 | 1 |
2023年CSP-J组复赛
2022年CSP-J组复赛
2021年CSP-J组复赛
2020年CSP-J组复赛
解题技巧
修改于 2025-10-18 05:11:30